

David Dương
Giới thiệu về bản thân


































+ Gọi x( x ≥ 0 ) là số kg loại I cần sản xuất,y ( y ≥ 0 ) là số kg loại II cần sản xuất.
Suy ra số nguyên liệu cần dùng là 2x+ 4y, thời gian là 30x+ 15y có mức lời là 40.000x+ 30.000y
Theo giả thiết bài toán xưởng có 200kg nguyên liệu và 120 giờ làm việc suy ra
2x+ 4y ≤ 200 hay x+ 2y- 100 ≤ 0 ; 30x+ 15y ≤ 1200 hay 2x+ y-80 ≤ 0
+ Tìm x; y thoả mãn hệ 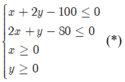
sao cho L( x; y) = 40.000x+ 30.000y đạt giá trị lớn nhất.
Trong mặt phẳng tọa độ vẽ các đường thẳng ( d) : x+ 2y-100= 0 và ( d’) : 2x+y-80=0
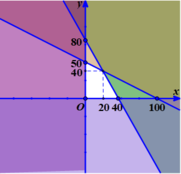
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tứ giác) không tô màu trên hình vẽ
Giá trị lớn nhất của L( x; y) đạt tại một trong các điểm (0; 0) ; (40; 0) ; (0; 50) ; (20; 40)
+ Ta có L(0; 0) = 0; L( 40; 0) =1.600.000;
L(0; 50) = 1.500.000; L(20; 40) = 2.000.000
suy ra giá trị lớn nhất của L(x; y) là 2.000.000 khi (x; y) =(20; 40).
Vậy cần sản xuất 20 kg sản phẩm loại I và 40 kg sản phẩm loại II để có mức lời lớn nhất.
+ Gọi x( x ≥ 0 ) là số kg loại I cần sản xuất,y ( y ≥ 0 ) là số kg loại II cần sản xuất.
Suy ra số nguyên liệu cần dùng là 2x+ 4y, thời gian là 30x+ 15y có mức lời là 40.000x+ 30.000y
Theo giả thiết bài toán xưởng có 200kg nguyên liệu và 120 giờ làm việc suy ra
2x+ 4y ≤ 200 hay x+ 2y- 100 ≤ 0 ; 30x+ 15y ≤ 1200 hay 2x+ y-80 ≤ 0
+ Tìm x; y thoả mãn hệ 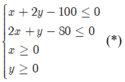
sao cho L( x; y) = 40.000x+ 30.000y đạt giá trị lớn nhất.
Trong mặt phẳng tọa độ vẽ các đường thẳng ( d) : x+ 2y-100= 0 và ( d’) : 2x+y-80=0

Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tứ giác) không tô màu trên hình vẽ
Giá trị lớn nhất của L( x; y) đạt tại một trong các điểm (0; 0) ; (40; 0) ; (0; 50) ; (20; 40)
+ Ta có L(0; 0) = 0; L( 40; 0) =1.600.000;
L(0; 50) = 1.500.000; L(20; 40) = 2.000.000
suy ra giá trị lớn nhất của L(x; y) là 2.000.000 khi (x; y) =(20; 40).
Vậy cần sản xuất 20 kg sản phẩm loại I và 40 kg sản phẩm loại II để có mức lời lớn nhất.
+ Gọi x( x ≥ 0 ) là số kg loại I cần sản xuất,y ( y ≥ 0 ) là số kg loại II cần sản xuất.
Suy ra số nguyên liệu cần dùng là 2x+ 4y, thời gian là 30x+ 15y có mức lời là 40.000x+ 30.000y
Theo giả thiết bài toán xưởng có 200kg nguyên liệu và 120 giờ làm việc suy ra
2x+ 4y ≤ 200 hay x+ 2y- 100 ≤ 0 ; 30x+ 15y ≤ 1200 hay 2x+ y-80 ≤ 0
+ Tìm x; y thoả mãn hệ 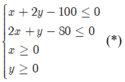
sao cho L( x; y) = 40.000x+ 30.000y đạt giá trị lớn nhất.
Trong mặt phẳng tọa độ vẽ các đường thẳng ( d) : x+ 2y-100= 0 và ( d’) : 2x+y-80=0

Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tứ giác) không tô màu trên hình vẽ
Giá trị lớn nhất của L( x; y) đạt tại một trong các điểm (0; 0) ; (40; 0) ; (0; 50) ; (20; 40)
+ Ta có L(0; 0) = 0; L( 40; 0) =1.600.000;
L(0; 50) = 1.500.000; L(20; 40) = 2.000.000
suy ra giá trị lớn nhất của L(x; y) là 2.000.000 khi (x; y) =(20; 40).
Vậy cần sản xuất 20 kg sản phẩm loại I và 40 kg sản phẩm loại II để có mức lời lớn nhất.
7cm
n= -1 ; -5 ; 1; 5
